Usage

Operating the Bin module is easy, with just one slider doing all the work.

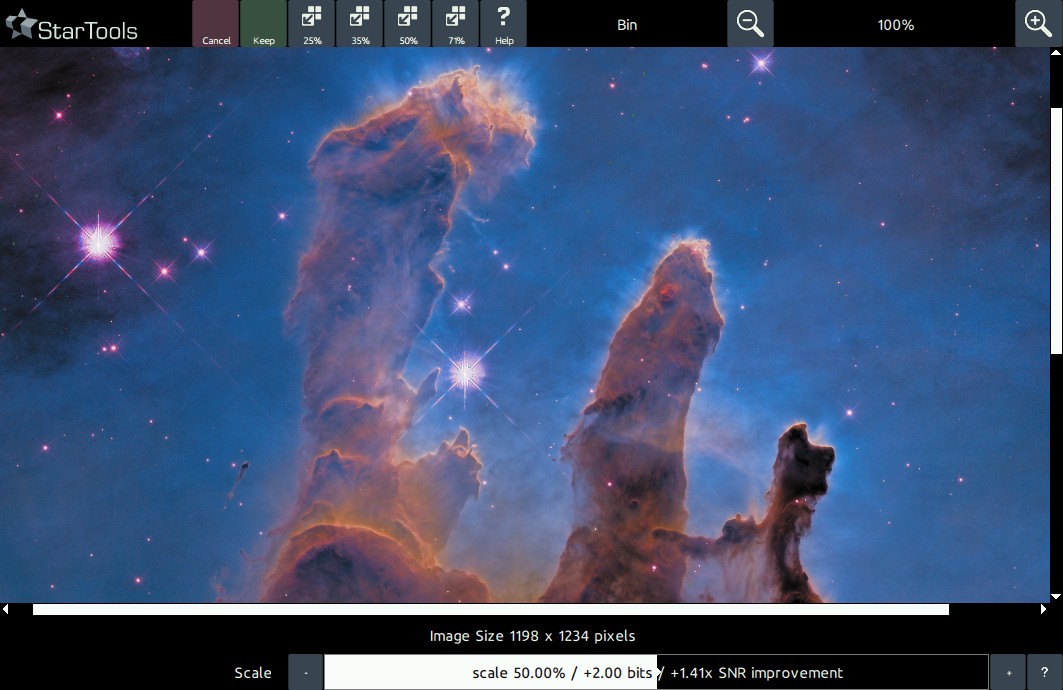
The Bin module is operated with just a single parameter; the 'Scale' parameter. This parameter controls the amount of binning that is performed on the data. The new resolution is displayed ('New Image Size X x Y') , as well the single axis scale reduction, the Signal-to-Noise-Ratio improvement and the increased bit-depth of the new image.

When to bin?

Data binning is a data pre-processing technique used to reduce the effects of minor observation errors. Many astrophotographers are familiar with the virtues of hardware binning. The latter pools the value of 4 (or more) CCD pixels before the final value is read. Because reading introduces noise by itself, pooling the value of 4 or more pixels reduces this 'read noise' also by a factor of 4 (one read is now sufficient, instead of having to do 4). Ofcourse, by pooling 4 pixels, the final resolution is also reduced by a factor of 4. There are many, many factors that influence hardware binning and Steve Cannistra has done a wonderful write-up on the subject on his starrywonders.com website. It also appears that the merits of hardware binning are heavily dependent on the instrument and the chip used.

Most OSCs (One-Shot-Color) and DSLR do not offer any sort of hardware binning in color, due to the presence of a Bayer matrix; binning adjacent pixels makes no sense, as they alternate in the color that they pick up. The best we can do in that case is create a grayscale blend out of them. So hardware binning is out of the question for these instruments.

So why does StarTools offer software binning? Firstly, because it allows us to trade resolution for noise reduction. By grouping multiple pixels into 1, a more accurate 'super pixel' is created that pools multiple measurements into one. Note that we are actually free to use any statistical reduction method that we want. Take for example this 2 by 2 patch of pixels;

7 7
3 7

A 'super pixel' that uses simple averaging yields (7 + 7 + 3 + 7) / 4 = 6. If we suppose the '3' is anomalous value due to noise and '7' is correct, then we can see here how the other 3 readings 'pull up' the average value to 6; pretty darn close to 7.

We could use a different statistical reduction method (for example taking the median of the 4 values) which would yield 7, etc. The important thing is that grouping values like this tends to filter out outliers and make your super pixel value more precise.

Binning and the loss of resolution

But what about the downside of losing resolution? That super high resolution may have actually been going to waste! If for example your CCD can resolve detail at 0.5 arcsecs per pixel, but your seeing is at best 2.0 arcsecs, then you effectively have 4 times more pixels than you need to record one 1 unit of real resolvable celestial detail. Your image will be "oversampled", meaning that you have allocated more resolution than the signal really will ever require. When that happens, you can zoom in into your data and you will notice that all fine detail looks blurry and smeared out over multiple pixels. And with the latest DSLRS having sensors that count 20 million pixels and up, you can bet that most of this resolution will be going to waste at even the most moderate magnification. Sensor resolution may be going up, but the atmosphere's resolution will forever remain the same - buying a higher resolution instrument will do nothing for the detail in your data in that case! This is also the reason why professional CCDs are typically much lower in resolution; the manufacturers rather use the surface area of the chip for coarser but more deeper, more precise CDD wells ('pixels') than squeezing in a lot of very imprecise (noisy) CCD wells (it has to be said the latter is a slight oversimplification of the various factors that determine photon collection, but it tends to hold).

Binning to undo the effects of debayering interpolation

There is one other reason to bin OSC and DSLR data to at least 25% of its original resolution; the presence of a bayer matrix means that (assuming an RGGB matrix) after applying a debayering (aka 'demosaicing') algorithm, 75% of all red pixels, 50% of all green pixels, and another 75% of all blue pixels are completely made up!

Granted, your 16MP camera may have a native resolution of 16 million pixels, however it has to divide these 16 million pixels up between the red, green and blue channels! Here is another very good reason why you might not want to keep your image at native resolution. Binning to 25% of native resolution will ensure that each pixel corresponds to one real recorded pixel in the red channel, one real recorded pixel in the blue channel and two pixels in the green channel (the latter yielding a 50% noise reduction in the green channel).

There are, however, instances where the interpolation can be undone if enough frames are available (through sub-pixel dithering) to have exposed all sub-pixels of the bayer matrix to real data in the scene (drizzling).

Fractional binning

StarTools' binning algorithm is a bit special in that it allows you to apply 'fractional' binning; you're not stuck with pre-determined factors (ex. 2x2, 3x3 or 4x4). You can bin exactly the amount that achieves a single unit of celestial detail in a single pixel. In order to see what that limit is, you simply keep reducing resolution until no blurriness can be detected when zooming into the image. Fine detail (not noise!) should look crisp. However, you may decide to leave a little bit of blurriness to see if you can bring out more detail using deconvolution.